1cm方眼を利用して面積が3,6,7平方センチメートルの正方形の作り方を教えてください!!コンパスを使っていいなら簡単で, いずれも「その正方形の辺の長さをどのように求めるか」という勝負になります1 3cm^2 の場合1 直径が (31)=正方形の面積 の部分一致の例文一覧と使い方 正方形 三角形の 面積 例文帳に追加 a unit of area, of which the standard is the area of a square whose side is one meter long EDR日英対訳辞書 また、1坪(歩)の 面積 の 正方形 の1辺が1間である。 例文帳に追加 In addition, the面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積 ・ 長方形の面積 ・ 台形の面積
初中数学 三个正方形的边长分别为a B 10 若ab 64 阴影部分的面积是多少 海燕数学 哔哩哔哩 つロ干杯 Bilibili
正方形 面積3
正方形 面積3-χ 2 +5χ+6=(χ+2)(χ+3) → (ばらばらの面積)=(たて)×(よこ) ← χ 2 +2χ-8=(χ-2)(χ+4) 正方形の場合は平方公式。(χ+3) 2 =χ 2 +6χ+9 次にやったのが,平方根。 2.平方根 → 8、本の話 面積が4の正方形の一辺の長さを求めなさい。この図形の面積を2通りの方法で出して、方程式を立てます。 「直角三角形×4」+「一辺 c c の正方形」=「一辺 a b a b の正方形」 ab 2 × 4 c2 = (a b)2 a b 2 × 4 c 2 = ( a b) 2 2ab c2 = a2 2ab b2 2 a b c 2 = a 2 2 a b b 2 c2 = a2 b2 c 2 = a 2 b 2 よって、直角三角形には c2 = a2 b2 c 2 = a 2 b 2 という関係式が成り立つことが導けました。 三平方の定理を直接証明する




面积的计算 长方形和正方形的面积ppt课件 Ppt课件下载 人人ppt
最大正方形 一辺が 1 cm のタイルが、H × W 個並べられています。 タイルは汚れているもの、綺麗なもののいずれかです。 綺麗なタイルのみを使ってできる正方形の面積の最大値を求めてください。正三角形の面積 三角形の面積(底辺と高さから) 三角形の面積(2辺と夾角から) 三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから)大きい正方形と小さい正方形の平均の面積を持つ正方形になります: このことを利用して面積3、6、7の正方形を描くことができます: 例えば左の図では、面積5の正方形の中の面積1の正方形の「向き」を コンパスで円を描いてそろえてあげて、
面積( )の正方形 面積( )の正方形 面積( )の正方形 ( 3 )それぞれの正方形の1辺の長さは、いつでも整数(この場合は自然数)で表せますか 。 平方根①平方根の意味a 学 年 3年 学習日: 月3 頂點 3 對角線 0 施萊夫利符號 {3} 考克斯特圖 ( 英語 : Coxeter diagram ) 對稱群 二面體群 (D 3), order 2×3 面積 內角(度) 60° 內角和 180° 對偶 正三邊形 (本身) 特性314×1=314 314×2=628 314×3=942 314×4=1256 314×5=157 314×6=14 314×7=2198 314×8=2512 314×9=26
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators正方形の面積の公式、対角線による求め方 正方形の面積の公式を下記に示します。 A= a 2 Aは正方形の面積、aは辺の長さです。皆さんご存知の公式ですが、実は、正方形の辺の長さでは無く「対角線の長さ」から求めることが可能です。 下図をみてください。正方形的面積是其邊長的平方。 如果邊長為 a ,那麼面積 A = a 2 {\displaystyle A=a^{2}} 。 如果我們知道正方形的對角線長 d ,那麼我們也可以之計算面積 A = d 2 2 {\displaystyle A={\frac {d^{2}}{2}}} ,如果正方形邊心距為r, 外接圓 半徑是R,那麼 A = 4 r 2 {\displaystyle A=4r^{2}} 。



长方形和正方形的面积计算课件3 人教版小学数学三年级下册课件 小学课件 中国儿童资源网



下面每个小方格都是边长1厘米的正方形 请你在方格纸上分别画一个长方形和一个正方形 并计算它们的面积 我画的长方形的面积 3平方厘米3平方厘米 正方形的 面积 4平方厘米4平方厘米 题目和参考答案 青夏教育精英家教网
外側の正方形の面積はどうかな? 半径10cmの円の外側に、正方形をかいて 円の面積のおよその大きさを考えよう 半径10cmの円の外側に正方形を書くと → 上の図のように、円の面積は、1辺10cmの正方形4つ分の面積より小さいことに気づかせます。円積問題(えんせきもんだい)とは古代の幾何学者たちによって定式化された「与えられた長さの半径を持つ円に対し、定規とコンパスによる有限回の操作でそれと面積の等しい正方形を作図することができるか」という問題である。 英語では円の正方形化 (squaring the circle) とも呼ばれる。右の図は,合同な正方形を3つ並べ て, その中に3本の直線を引いたもので す。 (1) EB:BDを求めなさい。 (2) 三角形CBEの面積 は, 正方形1個分の面積の何分のいくつです か。




长方形和正方形的面积 Ppt课件下载 Ppt模板 爱问共享资料




三年级数学下册 面积和面积单位 练习题 Doc 文档分享网
求積公式(平面) a=面積 正方形 長方形 平行四辺形 備考 a寸法はb辺に対し直角に測ったもの 直角三角形 凹んだ部分の長方形の面積は、 4×3=12㎠ 全体の長方形から凹んだ部分の長方形を引くので、 80㎠12㎠=68㎠ よって、 答え 68㎠ 別解 下の図のように補助線を入れることでも求めることができます。 このように3つの長方形に分けることができます。3 小学生が導き出す 手助け問題 31 (1) 三角形abcの面積;



长方形正方形面积的计算课件3 人教版小学数学三年级下册课件 小学课件 中国儿童资源网




正方形內部一點 求正方形面積 信欣茗數學園地 隨意窩xuite日誌
FdData 高校入試:中学数学3 年:三平方と平面図形 三平方の定理/特殊な直角三角形辺の比/正三角形・正六角形/その他/ 三平方と相似長さの計算 /直角三角形の2 つの鋭角に注目/ 面積の計算:高さが共通・底辺比→面積比/新しい正 六角形の面積を求めなさい。図の点Oは対称の中心です。 (開成中) $ $ 解答 (1) 外側の正方形の面積は,10 10 = 100(cm2) 内側の正方形の面積は外側の正方形の面積の 1 2 だから, 100 1 2 = 50(cm2)答 (2) 内側の正六角形の面積は,正六角形ABCDEFの面積の3 4 だから, 9 3 4 正方形の面積は、 a^2/2 で計算できちゃうよ。 つまり、 (対角線の二乗)÷2 ってわけだね。 たとえば、 対角線BDが10cmの正方形ABCDがあるとしよう。 この正方形の面積の求め方は、 (対角線)×(対角線)÷2 = 10×10÷2 = 50cm^2 になるんだ。 どう?? 公式



中考题 只知道长方形里3个三角形面积分别是2 3 4 求中间面积 网易视频



腾讯视频
面積 = 半径 × 半径 × 314 × 中心角 ÷ 360° 公式の 導出 ( どうしゅつ ) 方法と計算 例 ( れい ) は「 扇形の面積の求め方 」をご覧ください。 扇形の面積の求め方正八角形の対角線で囲まれた面積 東海中 08 円内を転がる正方形 雙葉中 07・6 転がる正方形 清真学園中 06・後期・3 長方形の通過する部分の面積など ラ・サール中 11・5 辺の通過する部分の面積 灘中正方形是特殊的平行四边形,也是特殊的长方形。在同一平面内:四条边都相等且一个角是直角的四边形是正方形 3 。 有一组邻边相等的矩形是正方形。 有一个角为直角的菱形是正方形。 正方形对角线相等
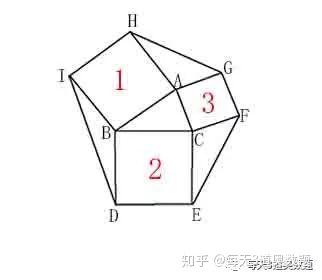



很经典的三角形外接正方形问题 18年5月30日 知乎



长方形和正方形面积的计算 Page33 西师大版三年级数学下册电子课本 教材 教科书 好多电子课本网
つまり、22、32、52のように平方数で割れるものを探せばいいのです。 ですから、素因数分解をすればいいわけです。 面積が8㎠の正方形 8 =2×2 ×2 =2×22 だから 8 = 2×22 =22 面積が18㎠の正方形 これは9分割すればいいから 18=2×3×3=2×32 だから 18 = 2×32 =321辺aの正五角形abcdeの中に正三角形fghを図のように内接させる。 ただし,cd∥hgとする。 正三角形の1辺の長さを求めよ。 (3) 1辺aの正五角形abcdeの中に正方形pqrsを図のように内接させる。 ただし,cd∥qrとする。 正方形の1辺の長さを求めよ。第27問 正方形5個の面積 図形ドリル 5年生 6年生 正方形 直角三角形 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。



三年级数学 长方形 正方形面积知识的综合应用 哔哩哔哩 つロ干杯 Bilibili




國中數學解題國二上2 3 畢氏定理正方形面積三等份tbcx凱爺數學 Youtube
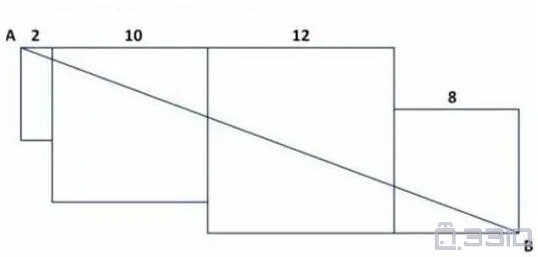
平方根応用 (図形)1,2,3 解説 1 図の ABCはAB=AC,∠BAC=90°の 直角二等辺三角形である。 頂点Aから辺BCに垂線をおろしその交点をPとする。 AP=2cm, BC=4cmのとき次の問いに答えよ。 (1) ABCの面積を求めよ。 もとの面積が1だったので、2つの直角二等辺三角形の面積は\(\frac{1}{2}\)ということが分かりますね。 左上の直角二等辺三角形を赤く塗ってみます。 同じようにした正方形をあと3つ準備します。 赤く塗った直角二等辺三角形が正方形になるように並べてみ 右側の正方形の一辺の長さは、x3、 です。 x (x8) (x3) = 25 x=12 となります。 真ん中の正方形の一辺の長さは、12cm、 左側の正方形の一辺の長さは、4cm、 右側の正方形の一辺の長さは、9cm、 よって、 真ん中の正方形の面積は、12cmの2乗=144c㎡、



三年级下册正方形公式 西瓜视频搜索



长方形与正方形面积计算 三 面积计算 奥数网
円の面積 円の面積は,半径×半径×314で求められます。 この求積公式の指導にあたっては,公式の理解はもとより,そこに至る過程を大切に指導することが重要です。 まず,半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるかを考え,下のように円の面積の見当をつけます。 つまり,円の面積は半径を1辺とする正方形の面積の2倍と4倍の 面積は当然、底辺×高さ× で求められるので、以下の通りです。 こうした一般的な解き方でも1分以内に解答したいところですが、今回教える2大公式によって高さ2秒、面積3秒、合わせて5秒で答えを出すことができます。 その公式がこちらです。 aに正此页面最后编辑于年3月18日 (星期三) 1133。 本站的全部文字在創用CC 姓名標示相同方式分享 30 協議 之條款下提供,附加條款亦可能應用(請參閱使用條款)。 Wikibooks®和維基教科書標誌是維基媒體基金會的註冊商標;維基™是維基媒體基金會的商標。 維基媒體基金會是在美國佛羅里達州登記



三年级下册正方形公式 西瓜视频搜索



下面每个小方格都是边长1厘米的正方形 请你在方格纸上分别画一个长方形和一个正方形 并计算它们的面积 我画的长方形的面积 3平方厘米3平方厘米 正方形的 面积 4平方厘米4平方厘米 题目和参考答案 青夏教育精英家教网
4年算数 大きい面積の求め方 子どもの学習支援 by いっちに算数 スマホ版 前のページに戻る 教え方4 平方メートル の単位を教え、平方メートル と平方センチメートル の単位の関係に気づかせます。 そのあとで、㎝とmの単位を混合した正方形や長方形の面積を求める問題を考えさせます。面積を二等分する直線 台形・平行四辺形の辺の中点 線分の3等分点 調和点列 点を通る平行線 平行線2 平行線3 円の接線 円外の点からの接線 New 点を通る垂線 New 面積が 1/5 の正方形 コンパスのみによ同様に他の3頂点も折ります.すると中に正方形pqrsができます.この正方形の面積はもとの正方形の面積の になります. md= ,am= ,pはaa'の中点だから pf= apbの面積 = ab×pf = ×1× = 正方形pqrsの面積 =正方形abcdの面積4× apbの面積



9厘米5厘米3厘米求正方形面积9厘米5厘米3厘米正方形面积是多少 答案圈



长方形 正方形面积的计算 人教版三年级下册数学电子课本 数九网
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題 面積3の正方形の作図 セルモに通っている生徒の多い近隣の喜多見中の数学では、テストの後 「数学レポート」 という、課題が出題されます。 塾長の私は、実は、この数学レポートの問題をいつも楽しみにしています。 今回は、作図の問題です。 面積4の方眼を利用して、面積3の正方形を作図しましょう。 の順に作図するとよい。 とあるので、少し考えてみ




使用蝴蝶模型巧解面积问题 蝴蝶模型的面积公式 双偶网



I2 Hdslb Com Bfs Archive 780d096b56b0fe96c86b



三年级数学 长方形 正方形的面积与周长 思维拓展 哔哩哔哩 つロ干杯 Bilibili



小学三年级周长面积练习题 松鼠文库



5a 3长方形正方形周长面积易错小练习1 5 松鼠文库



技巧 数学图形面积计算的十种方法 正方形
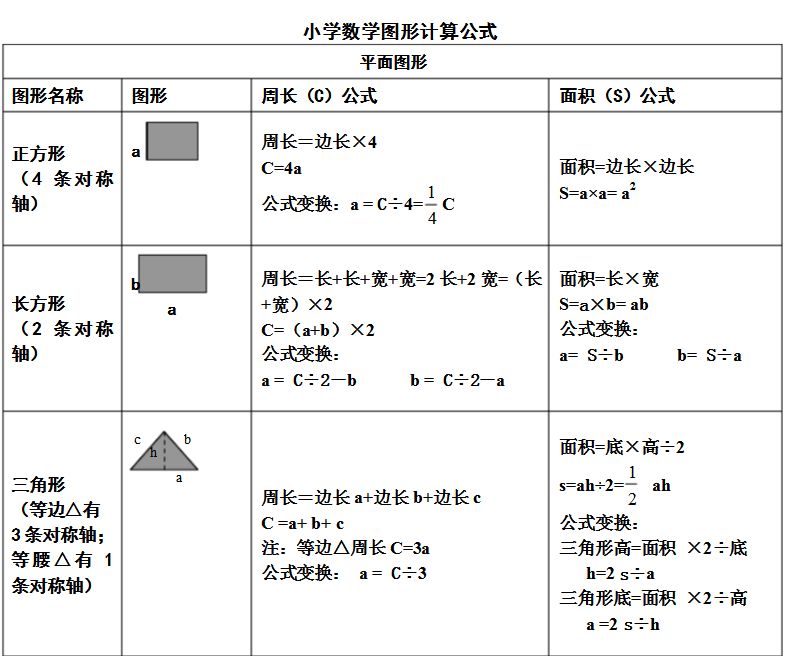



计算长方形的周长和面积公式 三年级数学上册长方形正方形计算公式及练习 附图形计算公式表 偷得一寸光的博客 Csdn博客




05 正方形的面積公式 Youtube



3 31长方形 正方形面积计算练习 哔哩哔哩 つロ干杯 Bilibili




正方形面積3 Youtube



长方形和正方形面积的计算 Page31 西师大版三年级数学下册电子课本 教材 教科书 好多电子课本网




三下长方形和正方形面积计算练习题 Doc 文档分享网




苏教版小学三年级数学下册 长方形和正方形的面积想想做做1 小学课本网



三年级 面积问题 边长加3增加39 求原正方形面积是多少 哔哩哔哩 つロ干杯 Bilibili




三年级数学下册 面积 专练 答案 长方形 正方形 组合图形 语文 网易订阅




正方形面積3 Youtube



小学三年级数学题 难倒985毕业生 你会吗 腾讯新闻



长 正方形面积的计算教案 三年级数学 小学数学 三a教育网



腾讯视频




三个正方形求阴影面积
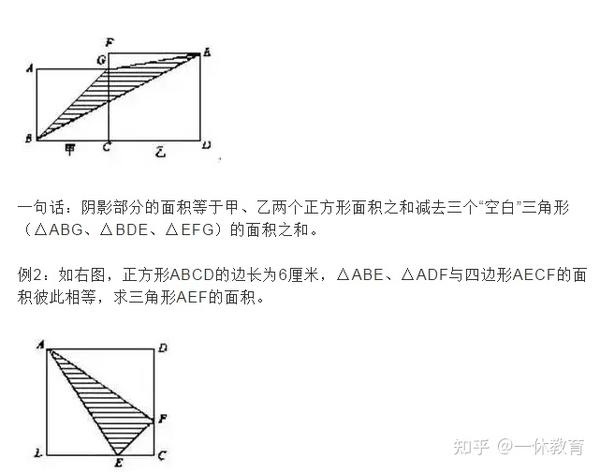



数学 小学数学必会图形求面积的10个方法 图文并茂 太神奇了 知乎



三下数学第六单元长方形 正方形面积计算练习课件 沃文网wodocx Com



初中数学 三个正方形的边长分别为a B 10 若ab 64 阴影部分的面积是多少 海燕数学 哔哩哔哩 つロ干杯 Bilibili



长方形与正方形面积计算 四 面积计算 奥数网



三年级数学长方形和正方形的面积练习题 Doc 沃文网wodocx Com




File 正方形内部一点到四顶点距离 与面积1 Jpg Wikimedia Commons




面積3の正方形の作図 セルモ大蔵 世田谷 の塾長ブログ




數學一點也不無聊 教學活動 圈正方形 搭配單元 二上畢氏定理
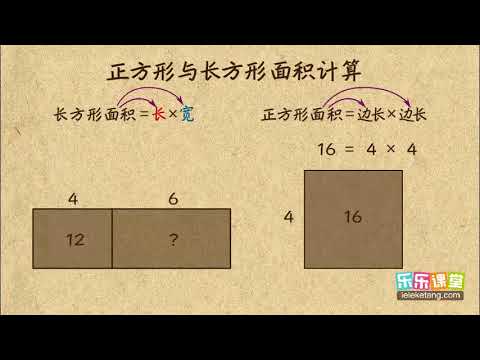



29 1 正方形 长方形面积计算小學奧數四年級幾何 Youtube



长方形 正方形面积的计算 Ppt课件下载 第一ppt



Data Wuyouwenku Com File Convert 21 03 24 14



正方形面积公式和周长 西瓜视频搜索



人教版小学三年级数学 面积知识点 辅课帮教育官网




三年级数学下册5面积第3课时长方形正方形面积的计算1课件新人教版下载 Ppt模板 爱问共享资料



三年级长方形与正方形面积练习题及答案 巧求周长 奥数网




面积单位 长方形和正方形的面积ppt课件3 Ppt课件下载 人人ppt




面积和面积单位 长方形和正方形的面积ppt课件 Ppt课件下载 人人ppt



1



5a 3长方形正方形周长面积分类小练习1 4 松鼠文库



四下翰林數學 周長與面積 Geometry Quiz Quizizz




正方形的周长公式 长方形正方形面积和周长的公式 三人行教育网 Www 3rxing Org



小学数学教师资格证面试 长方形和正方形的面积 人教版三年级下册 哔哩哔哩 Bilibili



正方形面积推导 西瓜视频搜索




瞇 當它是一個謎題 那麼 3呢



9厘米5厘米3厘米求正方形面积怎么算 抖音求正方形面积计算方法 图 特下载



腾讯视频



长方形 正方形面积的计算 面积ppt课件下载 第一ppt




苏教版小学三年级数学下册 长方形和正方形的面积想想做做3 小学课本网



初中数学竞赛题 直角三角形三边长3 4 5 求正方形面积 腾讯视频



小学三年级奥数题 长方形与正方形的面积 b 速算与巧算 奥数网



求面积三年级 万图壁纸网




9厘米5厘米3厘米求正方形面积怎么算 抖音求正方形面积计算方法 68游戏网




3种方法来计算正方形的周长



Q Tbn And9gcrc0zk5rndihxchrex0elksjk4vngxujtpo6ofscvvgs5perp6k Usqp Cau



1




面积的计算 长方形和正方形的面积ppt课件 Ppt课件下载 人人ppt



已知3个小长方形的面积 求三角形面积 你会吗 网易视频




46 面积入门和单位正方形 Youtube




三年级下册长方形正方形周长和面积应用题 附答案 正方体 网易订阅




三年级数学下册正方形的面积2教案冀教版教案下载 Word模板 爱问共享资料




长方形 正方形面积的计算 人教版三年级下册ppt课件下载 方木小哥




Pbs Twimg Com Media A31buc1ccaag7o3 Jpg



5a 3长方形正方形周长面积易错大练习1 3 松鼠文库



小升初的题目 怎么解 光谷社区



三年级长方形与正方形的面积专题练习



正方形面积公式小升初数学题求正方形面积 长方形和正方形的公式




3种方法来计算正方形的周长




3种方法来计算正方形的面积



5a 3长方形正方形周长面积分类小练习1 4 松鼠文库



A 33iq Com Upload 19 12 03 Thumbs Big



长方形变正方形三年级 西瓜视频搜索




數學一點也不無聊 教學活動 圈正方形 搭配單元 二上畢氏定理



中考题 只知道长方形里3个三角形面积分别是2 3 4 求中间面积 哔哩哔哩 Bilibili



利用三大技巧秒解复杂的面积计算问题 小学数学 学习资料大全 免费学习资源下载




新苏教版三年级下册数学 长方形和正方形的面积 练习试卷 302edu教育资源网



三角形def边长分别为3 4 5 求正方形abcd面积 很经典 哔哩哔哩 つロ干杯 Bilibili




已知正方形中三个三角形的面积分别为3



1




02正方形面積 Youtube



长方形和正方形的面积 Ppt 第一ppt




3种方法来计算正方形的周长



不规则正方形面积公式 西瓜视频搜索




苏教版小学三年级数学下册 长方形和正方形的面积练习 小学课本网




初二数学 3个正方形两两重叠 你知道怎么求阴影部分的面积吗 每日头条




三年级奥数长方形与正方形的面积专题练习 Doc 文档分享网




三年级数学下册 面积 专练 答案 长方形 正方形 组合图形 语文 网易订阅


